Expected Goals: wat is het en hoe berekenen we het?

32 miljoen euro. Dat is wat het Italiaanse Napoli betaalde voor Ajax-spits Arkadiusz Milik.

Ajax blij, Milik opgewekt naar het buitenland omdat hij mag gaan ravotten in het slim-fit shirtje van Napoli. En Napoli weer opgelucht dat ze die zak met geld van Higuain ergens aan konden besteden. Toch knap voor een club die in 2004 financieel schever stond dan de toren van Pisa. But who gives a shizzle? Napoli is back!

Even terug naar onze vriend Milik. Die had aan het einde van het eredivisie seizoen 2015/2016 een totale ExpG van 17,04.

Heu, ExpG van 17,04?

ExpG is een afkorting en staat voor ‘Expected Goals’ en is een statistische maat voor het verwachte aantal goals van een speler of team. Bij een ExpG wordt bij elke afzonderlijke doelpoging een waarde toegekend, gebaseerd op de kwaliteit van deze poging. Deze geeft aan hoevaak er gemiddeld genomen gescoord wordt vanuit een bepaalde positie. We belonen elke afzonderlijke poging van Milik met een ExpG waarde die ligt tussen de 0 en 1.

Een intikkertje van Milik heeft daarbij een veel grotere ExpG dan een schotpoging van ver buiten het penaltygebied, omdat die intikkers er simpelweg vaker in gaan. Bij een simpele punter van dichtbij zou je daarom een hogere ExpG (waarde dicht bij 1) verwachten, terwijl de ExpG van een lastig afstandsschot van buiten de 16 meter schommelt rond een ExpG van 0,02. Een afstandsschot vanuit een lastige positie gaat er immers niet zo vaak in.

Als we simpel gezegd alle 109 kansen en bijhorende ExpG van Milik op zouden tellen komen we uit op een totaal van 17,04 ExpG. Die optelsom van 17,04 is een theoretisch gemiddelde – op papier dus – want in werkelijkheid scoorde Milik er 21. Dat noemen we in de boekhouding efficiënt! Dit zijn namelijk vier treffers meer dan wat we normaal gesproken zouden verwachten gezien de kansen en kwaliteit daarvan.

Ja oké, maar hoe wordt elke afzonderlijke doelpoging van Milik omgezet naar een ExpG-waarde?

Om deze vraag te beantwoorden gebruiken we de data van alle spelers en alle wedstrijden in het eredivisieseizoen 2015/2016. Een doelpoging heeft altijd twee mogelijke uitkomsten. Een speler rammelt die bal erin of hij doet dat niet. Deze (dan wel of geen) goal noemen we voor het gemak de uitkomst. Een dichotome uitkomst omdat er maar twee mogelijkheden zijn, namelijk ‘wel’ of ‘geen’ goal uit een poging. Een statistisch model dat geschikt is bij het analyseren van zo`n dichotome uitkomst is een ‘logistische regressie’.

Buiten de uitkomst (wel/geen goal) willen we ook heel graag weten wat de goalverwachting (ExpG) is van bijvoorbeeld een afstandsschot of een kopbal uit een corner. Of wat is nu een ExpG die hoort bij een vrije trap. Zoals eerder al vermeld wordt de hoogte van de ExpG bepaald door de kwaliteit van deze doelpoging. De kwaliteit van de doelpogingen meten we aan de hand van verschillende variabelen. We lopen ze hieronder stuk voor stuk na met uitleg en illustratie.

Laten we bij die uitleg als eerste beginnen met een van de belangrijkste variabelen binnen het model: de afstand van de doelpoging tot het doel. In de onderstaande afbeelding is afstand in meters (op de onderste as) afgezet tegenover de berekende ExpG. Elk zwart puntje binnen de afbeelding is een doelpoging. Het zijn er iets meer dan 8100: zoveel doelpogingen zijn er door alle spelers in alle wedstrijden binnen de eredivisie in seizoen 2015/2016 ondernomen.

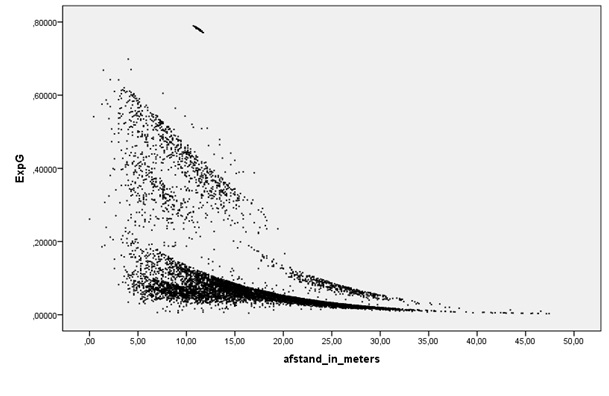
Wat we zien is dat de ExpG aanzienlijk daalt wanneer de afstand tot het doel groter wordt. Keepers hebben bij een afstandsschot over het algemeen meer reactie tijd voor een redding. De goalverwachting van afstandsschot buiten het strafschopgebied brokkelt mede hierdoor al snel af tot onder de 4 procent. Anders gezegd: Een gokkastje in het buurtcafé dat na 25 keer drukken 1 keer uitbetaald. Een afstandsschot is in werkelijkheid dus een statistische `big fat nothing`. Waarom veel spelers toch schieten van grote afstand? Een afstandsschot wordt vaak door een voetballer binnen het topvoetbal instinctief en in een splitsecond genomen. Michiel de Hoog, Sportredacteur van de Correspondent, schreef er een verdiepend stuk over met de veelzeggende titel `waarom FC Utrecht trainer Erik ten Hag liever geen afstandsschoten ziet`.

Lichaamsdeel

Is er binnen het model ook nog een onderscheid gemaakt tussen verschillende soorten doelpogingen? Kort gezegd, ja. Iedere poging (zwart stipjes) in de eerste diagram kunnen we voorzien van een kleur om de verschillende pogingtypes wat te verduidelijken. In de afbeelding hieronder zijn de pogingen met het hoofd in het groen aangeven.

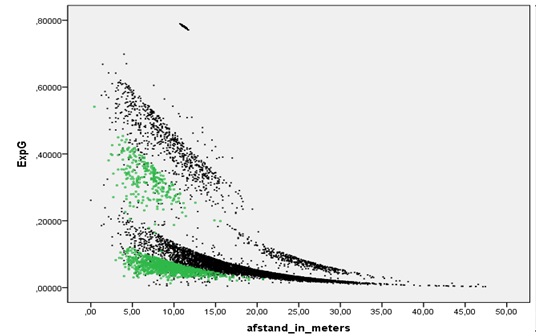
Interessant is om spelers specifiek te bekijken op doelpogingen met alleen dit lichaamsdeel. Welke voetballers weten met de kop veel en betere kansen te creëren? Of welke spelers hebben relatief een hoge ExpG met het hoofd? Als we voetballers uit Eredivisie alleen op kopkansen beoordelen dan springen er een aantal letterlijk boven uit. Het zijn vooral erkend sterke koppers binnen de competitie. Mike Havenaar en Luuk de Jong, dat soort jongens, maar let dit seizoen zeker ook eens op Vincent Vermeij van Heracles.

En schoten? Die pogingen zijn visueel gemaakt in het zwart. Schoten krijgen binnen het statistisch model een iets hogere ExpG toegekend in vergelijking tot kopballen. De theorie hierachter is dat er bij een schot meer kracht en richtingscontrole kan worden uitgeoefend door een speler. Daarbij ben je bij een kopbal ook altijd nog afhankelijk van een goede voorzet. Een schot gaat er over het algemeen vaker in dan een kopbal op dezelfde afstand van het doel.

Grote kansen

Buiten afstand en lichaamsdeel worden ook ‘grote kansen’ meegenomen. Een ‘grote kans’ is een typering die dataprovider OPTA gebruikt in spelsituaties waar een speler in redelijkheid had mogen scoren. Vaak zijn dit 1 op 1 scenario’s met de keeper en pogingen dicht op het doel. 13 procent van de doelpogingen is een ‘grote kans’ en 4 van de 10 keer wordt er in deze situatie-definitie gescoord. Het is samen met afstand de belangrijkste voorspeller op een goal. Een grote kans verhoogt je ExpG aanzienlijk. Een `Michael Knight turbo boost`.

Gevolg is wel dat deze OPTA definitie een erg bepalende rol heeft binnen het ExpG model. In de afbeelding hieronder is een duidelijke scheidinglijn aanwezig tussen grote kansen (in het rood) en kansen die helaas niet voldoen aan deze typering (in het zwart).

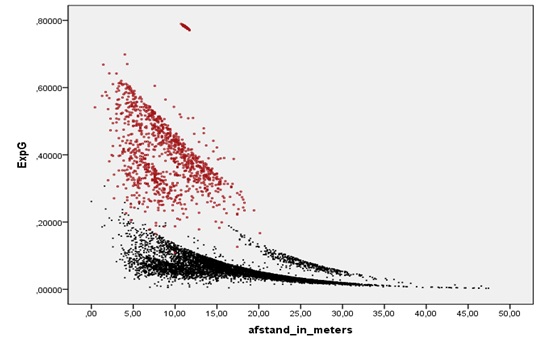
Doelpogingen zonder dit OPTA keurmerk komen niet uit boven een ExpG van 0,30. Zo is als voorbeeld de hoge ExpG (15,12) van Mike Havenaar binnen de Eredivisie deels te verklaren door zijn veelheid aan grote kansen. Van de 81 doelpogingen wist hij er totaal 29 te turbo boosten met deze OPTA definitie. Dat is welgeteld 36%. Relatief een behoorlijk contrast met pak hem beet Hakim Ziyech, die van de 157 pogingen er 9 wist te creëren. Omgerekend is dat 6% aan grote kansen voor deze nieuwe aanwinst van Ajax. De ExpG (13,08) van Ziyech valt hierdoor wat tegen gezien zijn hoeveelheid kansen. Sterker nog…… niemand schoot zo vaak als Ziyech binnen de Eredivisie, maar er waren wel spelers die vaker scoorden. Ziyech schoot voornamelijk van afstand.

Vrije trappen en penalty’s

Er blijven binnen het model nog twee primaire pogingstypes over, namelijk directe vrije trappen en penalty`s. Vrije trappen zijn geïllustreerd in het oranje en hebben binnen de eredivisie gemiddeld een kleine 8% kans op een doelpunt. Het succes van een directe vrijetrap is afhankelijk van behoorlijk wat factoren. Je kunt daarbij denken aan schottechniek, balsnelheid en locatie. Binnen het ExpG model wordt alleen afstand en hoek als meting meegenomen. De afstand van de vrijetrap heeft een negatief effect op de goal verwachting. Hoe groter de afstand van een vrijetrap hoe kleiner de kans op een goal.

De langere reactietijd van een goalkeeper speelt ook hierin een belangrijke rol. De ExpG van een directe vrijetrap ligt wel wat hoger dan een normaal schot uit een vergelijkbare positie. De ExpG van een normaal schot uit open spel ligt op een gemiddelde van 4 procent. Dat de ExpG van een vrijetrap twee keer zo zwaar telt als een normaal schot kan worden verklaard uit de privileges van de vrijetrap. Bij een directe vrijetrap krijgt een specialist de tijd om een bal te plaatsen. De hoek tot het doel is juist wel weer een pluspuntje voor de ExpG. De verwachting dat een penalty er in gaat, ligt op plusminus 78%. Penalty`s zijn in het lichtblauw aangegeven.

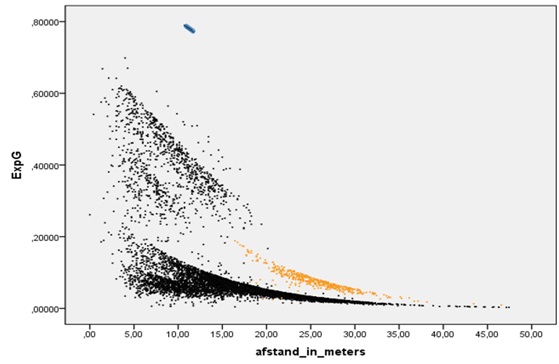
Secundaire spelsituaties

Buiten de primaire doelpogingen zijn er ook nog ‘secundaire spelsituaties’. Hierbij kun je denken aan counters, corners en pogingen uit een indirecte standaardsituatie. Van deze drie situaties heeft de corner het meeste statistisch effect. Dit effect is weliswaar negatief waardoor we kunnen zeggen dat een doelpoging vanuit een corner de ExpG eerder wat verlaagt.

Een schot van Dirk Kuyt heeft een hogere ExpG dan precies dat zelfde schot van Dirk uit een corner. Verklaring voor dit negatief corner-effect is dat een strafschopgebied vaak vol gestouwd staat met spelers. Gevolg is dat er voor goede koppers en schutters weinig bewegingsruimte is/ontstaat om te scoren.

Counters hebben op zichzelf een (klein) positief invloed op de ExpG. Vier van de tien keer is een snelle omschakeling een ‘grote kans’. Wel worden de grote kansen vanuit een snelle uitbraak minder goed uitgespeeld. Normaal benut men uit open spel een grote kans in 40% van de gevallen, bij een grote kans vanuit een counter is dat slechts 31%. Misschien heeft de erg hoge snelheid tijdens een counter negatieve invloed op de efficiënte afronding. Counters worden bijna altijd uitgespeeld met de voet. Van de 74 counters kopte alleen Roda JC speler Richmond Boakye de bal (naast het doel). En indirecte standaardsituaties? Geen noemenswaardig effect.

Ter afsluiting (Milik)

Keren we tot slot nog even terug naar Arkadiusz Milik. Zijn totale goalverwachting (ExpG is 17,04) was opgebouwd uit 109 doelpogingen. We filteren Milik uit het databestand om zijn ExpG nog wat uit de doeken te doen. In de laatste diagram hieronder zijn alle pogingen van Milik weergegeven.

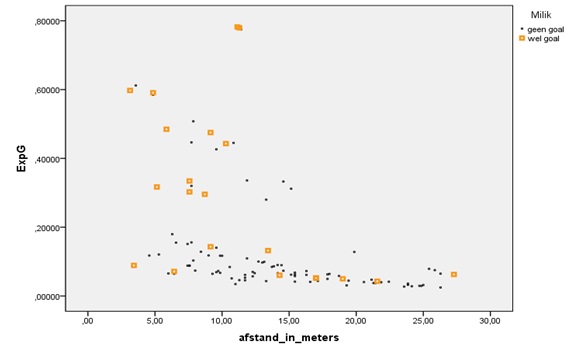
Milik tikte in werkelijkheid 21 treffers af in het seizoen 2015/2016. Dat is 4 goals boven zijn theoretische verwachting (ExpG) van 17,04. Hij is hierin als voetballer zeker geen uitzondering. Goede spelers weten hun ExpG vaker te overklassen, althans daar mag je van uitgaan. Dit gezien het feit dat het concept ExpG niets meer is dan een benchmark. Wat je zou mogen verwachten van een (gemiddelde) eredivisiespeler gezien de kansen en kwaliteit daarvan.

109 doelpogingen, 21 goals en een ExpG van 17,04. Napoli had er uiteindelijk 32 miljoen voor over. Een EK effect, transfertombola, wat het ook mag zijn, er werd nog nooit zo veel geld overgemaakt naar de Amsterdam Arena. Ajax was er blij mee.